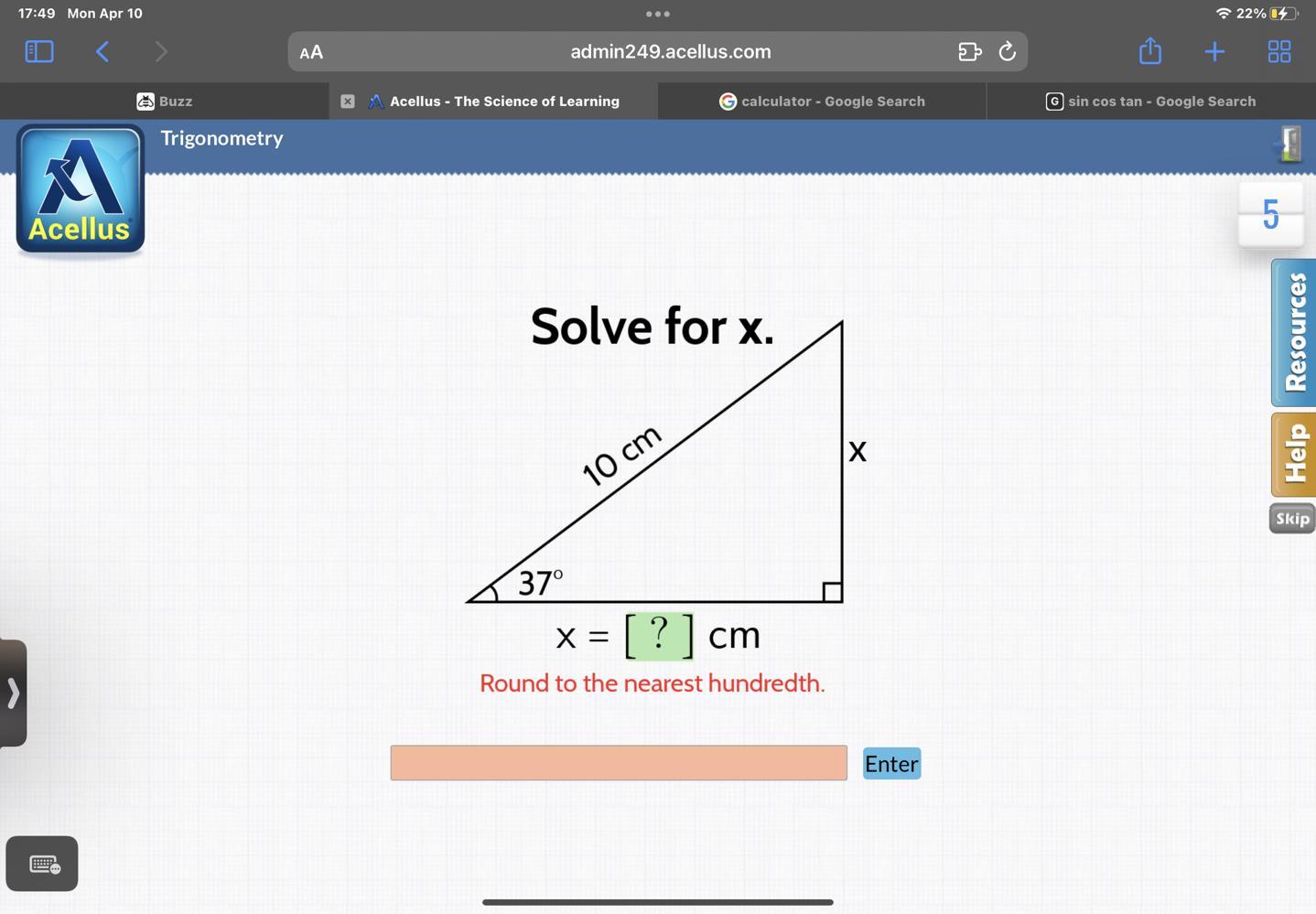
Answers
Answer:
6.02
Step-by-step explanation:
sin 37=x/10
x/10=sin 37
x=10(sin 37)
x=6.02
Related Questions
Can someone help me ASAP? It’s due today
Answers
The only option that represents an independent event is: Option C: "Spinning a Spinner with eight evenly spaced sections, then spinning it again.".
How to Identify Independent Events?Independent events are defined as those events whose occurrence is not dependent on any other event. For example, if we flip a coin in the air and get the outcome as Head, then again if we flip the coin but this time we get the outcome as Tail. In both cases, the occurrence of both events is independent of each other.
Looking at the given options, the only one that represents an independent event is "Spinning a Spinner with eight evenly spaced sections, then spinning it again.".
This is because each event does not depend on another one of the events being described.
Read more about Independent Events at: https://brainly.com/question/22881926
#SPJ1
Find the solution to the system of equations. Write the solution as an ordered pair. If there are no solutions, write 'no solutions'. If there are infinitely many, write 'infinitely many'.
y = −72
x + 11
7x + 2y = 20
Answers
The solution to the system of equations is (23, -72).
How to find system of equations ?The first equation is y = -72, which means that whatever the value of x is, the value of y will always be -72.
Substituting y = -72 in the second equation, we get:
7x + 2(-72) = 20
Simplifying this equation, we get:
7x - 144 = 20
Adding 144 to both sides, we get:
7x = 164
Dividing both sides by 7, we get:
x = 23.428571...
So the solution to the system of equations is the ordered pair (x, y) = (23.428571..., -72).
However, we usually express solutions as ordered pairs of integers, so we can round x to the nearest integer to get:
(x, y) = (23, -72)
Therefore, the solution to the system of equations is (23, -72).
Learn more about system of equations here:https://brainly.com/question/25976025
#SPJ1
Solve x^2 + 6x + 9 = 0 by graphing. Please enter the number part of your answer only.
If your answer has two numbers, enter them like this: x = 6 and -1 should be entered as "6, -1" (no quotes).
Answers
Answer:
-3
Step-by-step explanation:
You want the graphical solution to x² +6x +9 = 0.
GraphThe graph of the expression on the left shows it has a value of 0 when x = -3.
The solution is x = -3.
__
Additional comment
A graphing calculator is very helpful when you want a graphical solution.
If you want to graph this by hand, you can rewrite it as ...
(x +3)² = 0
The graph of (x +3)² is a graph of the parent function y = x² after it has been shifted left 3 units. The graph will go through points (-5, 4), (-4, 1), (-3, 0), (-2, 1), (-1, 4). Of course the point at (-3, 0) indicates the solution is x=-3.
For the function 8-(x-3)^2,
state the domain
Answers
The domain of the function 8 - [tex](x-3)^{2}[/tex] is R which is all the real numbers.
What is domain of a function?
The set or grouping of all potential values that may be used in the function is known as the domain.
We are given a function as 8 - [tex](x-3)^{2}[/tex].
Now, in order to find the domain, we need to find the values where the function is not defined for a value of x.
But, there is no such value for x where the function is not defined.
This means that all values of x give an output.
So, the domain is the set of all the real numbers.
Hence, the domain of the given function is R.
Learn more about domain of function from the given link:
https://brainly.com/question/1369616
#SPJ1
Distance between (7,-2) and (-1,-1)
Answers
Answer: The distance formula between two points (x1, y1) and (x2, y2) is:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Using this formula, we can find the distance between (7, -2) and (-1, -1):
d = sqrt((-1 - 7)^2 + (-1 - (-2))^2)
= sqrt((-8)^2 + (1)^2)
= sqrt(64 + 1)
= sqrt(65)
Therefore, the distance between (7, -2) and (-1, -1) is sqrt(65), or approximately 8.06 units.
Step-by-step explanation:
which expressions are equivalent to 8 13 ?
Answers
The next four equivalent fractions of 8/13 are:
16/2624/3932/5240/65What are some equivalent fractions of 8/13?Equivalent fractions are fractions that represent the same value but have different numerator and denominator. To find equivalent fractions of 8/13, we can multiply both the numerator and the denominator by the same non-zero integer.
In this case, we multiplied the numerator and denominator by 2, 3, 4, and 5, respectively, to obtain the next four equivalent fractions: 16/26, 24/39, 32/52, and 40/65. These fractions have different numerators and denominators, but they are equivalent to 8/13 as they represent the same value or amount.
Read more about equivalent expression
brainly.com/question/15775046
#SPJ1
I will be given brainliest!!!!
Answers
Answer:2/3
Step-by-step explanation:
its the only possible answer because it needs to have a scale factor below one as A'B'C'D' is smaller than ABCD
Answer: 2/3
Step-by-step explanation:
The corresponding side of AD is A'D'.
AD = 30
A'D' = 20
Scale factor = 2/3 because AD * 2/3 = A'D'
If I'm wrong, please tell me.
Hello solve this, what is 9 x 5/7
Answers
Answer: 6 3/7
Step-by-step explanation:
9/1 x 5/7
If we multiply the numerators and denominators, we get 45/7 or 6 3/7 as a mixed number.
Answer:
[tex]\frac{45}{7}[/tex] or 6.4285
Step-by-step explanation:
First, multiply 9 and 5, which gives you 45.
9(5)=45
Then, divide 45 by 7.
45/7=6.4285
That gives you [tex]\frac{45}{7}[/tex] or 6.4285
Hope this helps!
In a race, 14 out of the 25 swimmers finished in less than 47 minutes. What percent of swimmers finished the race in less than 47 minutes? Write an equivalent fraction to find the percent.
Answers
We must first convert the given information into an equivalent fraction. The answer is 56%.
What is equivalent fraction?Equivalent fractions have the same value or represent the same portion of a whole even though they may have different numerators and denominators.
To do this, we must multiply both the numerator (14) and denominator (25) by the same number so that the denominator equals 100.
To do this, we must multiply both 14 and 25 by 4.
This gives us 14*4/25*4 = 56/100.
To convert this fraction to a percent, we can simply divide the numerator by the denominator and multiply the result by 100.
Therefore, 56/100 * 100 = 56%.
This result can also be found by setting up a proportion. We can set up the proportion as follows:
14/25 = x/100.
To solve for x, we must multiply both sides by 100. This gives us 14*100/25 = x.
Hence, x = 56. Therefore, 56% of swimmers finished the race in less than 47 minutes.
For more questions related to proportion
https://brainly.com/question/1496357
#SPJ1
Find the value of x .
J
30°
M
to
K
(2x - 30)°
[
Answers
The value of x in the Intersecting chords is 15
Finding the value of x .From the question, we have the following parameters that can be used in our computation:
Intersecting chords
The value of x is then calculated as
x = 1/2(30 - 2x + 30)
So, we have
2x = 30 - 2x + 30
Evaluate the like terms
4x = 60
Divide
x = 15
Hence, the value of x is 15
Read more about angles at
https://brainly.com/question/28293784
#SPJ1
need answer by 11:45am
The box plots display measures from data collected when 20 people were asked about their wait time at a drive-thru restaurant window.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 8.5 to 15.5 on the number line. A line in the box is at 12. The lines outside the box end at 3 and 27. The graph is titled Super Fast Food.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 9.5 to 24 on the number line. A line in the box is at 15.5. The lines outside the box end at 2 and 30. The graph is titled Burger Quick.
Which drive-thru typically has more wait time, and why?
Burger Quick, because it has a larger median
Burger Quick, because it has a larger mean
Super Fast Food, because it has a larger median
Super Fast Food, because it has a larger mean
Question 3
A charity needs to report its typical donations received. The following is a list of the donations from one week. A histogram is provided to display the data.
5, 5, 6, 8, 10, 15, 18, 20, 20, 20, 20, 20, 20
A graph titled Donations to Charity in Dollars. The x-axis is labeled 1 to 5, 6 to 10, 11 to 15, and 16 to 20. The y-axis is labeled Frequency. There is a shaded bar up to 2 above 1 to 5, up to 3 above 6 to 10, up to 1 above 11 to 15, and up to 7 above 16 to 20.
Which measure of variability should the charity use to accurately represent the data? Explain your answer.
The range of 13 is the most accurate to use, since the data is skewed.
The IQR of 13 is the most accurate to use, since the data is skewed.
The range of 20 is the most accurate to use to show that they have plenty of money.
The IQR of 20 is the most accurate to use to show that they need more money.
Question 4
The circle graph describes the distribution of preferred transportation methods from a sample of 400 randomly selected San Francisco residents.
circle graph titled San Francisco Residents' Transportation with five sections labeled walk 40 percent, bicycle 8 percent, streetcar 15 percent, bus 10 percent, and cable car 27 percent
Which of the following conclusions can we draw from the circle graph?
Together, Streetcar and Cable Car are the preferred transportation for 168 residents.
Together, Walk and Streetcar are the preferred transportation for 55 residents.
Bus is the preferred transportation for 45 residents.
Bicycle is the preferred transportation for 50 residents.
Question 5
The line plot displays the number of roses purchased per day at a grocery store.
A horizontal line starting at 1 with tick marks every one unit up to 10. The line is labeled Number of Rose Bouquets, and the graph is titled Roses Purchased Per Day. There is one dot above 1 and 2. There are two dots above 8. There are three dots above 6, 7, and 9.
Which of the following is the best measure of variability for the data, and what is its value?
The range is the best measure of variability, and it equals 8.
The range is the best measure of variability, and it equals 2.5.
The IQR is the best measure of variability, and it equals 8.
The IQR is the best measure of variability, and it equals 2.5.
Question 6
The histograms display the frequency of temperatures in two different locations in a 30-day period.
A graph with the x-axis labeled Temperature in Degrees, with intervals 60 to 69, 70 to 79, 80 to 89, 90 to 99, 100 to 109, 110 to 119. The y-axis is labeled Frequency and begins at 0 with tick marks every one unit up to 14. A shaded bar stops at 10 above 60 to 69, at 9 above 70 to 79, at 5 above 80 to 89, at 4 above 90 to 99, and at 2 above 100 to 109. There is no shaded bar above 110 to 119. The graph is titled Temps in Sunny Town.
A graph with the x-axis labeled Temperature in Degrees, with intervals 60 to 69, 70 to 79, 80 to 89, 90 to 99, 100 to 109, 110 to 119. The y-axis is labeled Frequency and begins at 0 with tick marks every one unit up to 16. A shaded bar stops at 2 above 60 to 69, at 4 above 70 to 79, at 12 above 80 to 89, at 6 above 90 to 99, at 4 above 100 to 109, and at 2 above 110 to 119. The graph is titled Temps in Desert Landing.
When comparing the data, which measure of center should be used to determine which location typically has the cooler temperature?
Median, because Desert Landing is symmetric
Mean, because Sunny Town is skewed
Mean, because Desert Landing is symmetric
Median, because Sunny Town is skewed
Question 7
At a recent baseball game of 5,000 in attendance, 150 people were asked what they prefer on a hot dog. The results are shown.
Ketchup Mustard Chili
63 27 60
Based on the data in this sample, how many of the people in attendance would prefer mustard on a hot dog?
900
2,000
2,100
4,000
Answers
The drive-thru with typically more wait time is Burger Quick, because it has a larger median. The Option A.
Why does Burger Quick have a larger median for wait time?The median is a measure of central tendency that represents the middle value of a set of data. In this case, the median wait time at Burger Quick is 15.5 minutes, while the median wait time at Super Fast Food is 12 minutes.
This indicates that, on average, customers at Burger Quick experience a longer wait time compared to customers at Super Fast Food. The larger median at Burger Quick suggests that there may be some longer wait times skewing the data towards the higher end which could be due to various factors such as slower service, or other operational issues at Burger Quick resulting in a longer wait time for customers at their drive-thru.
Read more about median
brainly.com/question/16408033
#SPJ1
Solve for length of segment d.
= 4 cm
b = 12 cm
c = 6 cm
4. ? =
].d
Enter the segment length tha
belongs in the green box.
If two segments intersect inside
or outside a circle: ab = cd
Answers
Answer: Using the given information and the formula ab = cd, we can write:
d = (ab) / c
We are given b = 12 cm and c = 6 cm. To find ab, we can use the Pythagorean theorem:
a^2 + b^2 = c^2
where a is the unknown length we want to find. Substituting the given values, we get:
a^2 + 12^2 = 6^2
a^2 + 144 = 36
a^2 = -108 (which is not a possible solution)
This means that the given values do not form a valid triangle. Therefore, we cannot find the length of segment d using the given information.
Step-by-step explanation:
Complex numbers [tex]z[/tex] and [tex]w[/tex] satisfy [tex]|z|=|w|=1, |z+w|=\sqrt{2}[/tex].
What is the minimum value of [tex]P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|[/tex]?
Answers
Okay, here are the steps to find the minimum value of P:
1) Given: |z|=|w|=1 (z and w are complex numbers with unit modulus)
|z+w|=sqrt(2)
Find z and w such that these conditions are satisfied.
Possible solutions:
z = 1, w = i (or vice versa)
z = i, w = 1 (or vice versa)
2) Substitute into P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|
For the cases:
z = 1, w = i: P = |-1-4+2(1+i)i| = |-5+2i| = sqrt(25+4) = 5
z = i, w = 1: P = |1-\frac{4}{i}+2(1+\frac{1}{i})i| = |-3+2i| = sqrt(9+4) = 5
3) The minimum value of P is 5.
So in summary, the minimum value of
P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|
is 5.
Let me know if you have any other questions!
Lin plans to swim 12 laps in the pool. She has swum 9.75 laps so far.
How many laps does she have left to swim? Use y
for the number of laps that Lin has left to swim.
Answers
Lin plans to swim 12 laps and has already swum 9.75 laps, so the number of laps she has left to swim can be found by subtracting 9.75 from 12:
y = 12 - 9.75
Simplifying the right side:
y = 2.25
Therefore, Lin has 2.25 laps left to swim.
Joey deposits $6000 each into the two savings accounts described below. If he doesn’t make any other deposits or withdrawals, find the combined amount of accounts after 10 years.
Account 1
3.5% annual simple interest
Account 2
3.5% annual compound interest
Answers
The combined amount in both accounts after 10 years is $16,869.58
What is formula of simple interest and compound interest ?To solve the problem, we need to use the following formulas:
Simple Interest = Principal x Rate x Time
Compound Interest = [tex]Principal * (1 + Rate/ n)^{n * Time}[/tex]
where:
Principal = the initial deposit
Rate = the interest rate (in decimal form)
Time = the number of years
n = the number of times interest is compounded per year
For Account 1:
Simple Interest = Principal x Rate x Time
= $6000 x 0.035 x 10
= $2100
The amount in Account 1 after 10 years will be the initial deposit plus the interest earned:
= $6000 + $2100
= $8100
For Account 2:
Since the interest is compounded annually, n = 1.
Compound Interest = [tex]Principal * (1 + Rate/ n)^{n * Time}[/tex]
= [tex]6000 *(1 + 0.035/1)^{1 * 10}\\= $6000 (1.035)^{10}\\= $8769.58[/tex]
After ten years, the amount in Account 2 will be $8769.58.
After ten years, the combined amount in both accounts will be:
$8100 minus $8769.58 equals $16869.58, resulting in a total of $16,869.58 in both accounts after ten years.
know more about simple interest visit:
https://brainly.com/question/25845758
#SPJ1
Solve for x please
Choices are...
10
5
25
90
Answers
Answer:
x = 10
Step-by-step explanation:
Angle form is = 90°
therefore
5x + 25 + x + 5 = 90
6x + 30 = 90
6x = 90-30
6x = 60
6x/6 = 60/6
x = 10
Which equations represent circles that have a diameter of 12 units and a center that lies on the y-axis? Select two options. x2 + (y – 3)2 = 36 x2 + (y – 5)2 = 6 (x – 4)² + y² = 36 (x + 6)² + y² = 144 x2 + (y + 8)2 = 36
Answers
The two options that represent circles with diameter 12 units and center on the y-axis are:
x² + (y - 6)² = 36
x² + (y + 6)² = 36
What is circles diameter?The diameter of a circle is a straight line segment that passes through the center of the circle and connects two points on its circumference. It is twice the length of the circle's radius.
The equations that represent circles that have a diameter of 12 units and a center that lies on the y-axis are:
x² + (y - 6)² = 36
x² + (y + 6)² = 36
Explanation:
For a circle with diameter 12 units, the radius is half of the diameter, which is 6 units.
Since the center of the circle lies on the y-axis, the x-coordinate of the center is 0.
The general equation for a circle with center (h, k) and radius r is (x - h)² + (y - k)² = r².
Using the given information, we substitute h = 0, k = ±6, and r = 6 to get the two equations:
(x - 0)² + (y - 6)² = 6² => x² + (y - 6)² = 36
(x - 0)² + (y + 6)² = 6² => x² + (y + 6)² = 36
Therefore, the two options that represent circles with diameter 12 units and center on the y-axis are:
x² + (y - 6)² = 36
x² + (y + 6)² = 36
To know more about circles diameter visit:
https://brainly.com/question/28162977
#SPJ1
what is the surface are of a cylender when the radius is 6in and the height is 9 in
Answers
Answer:
565.486677646 inches squared
Step-by-step explanation:
Let's recall the formula for the surface area of a cylinder:
[tex]A=2\pi rh+2\pi r^2[/tex]
Where r is the radius and h is the height.
We are given that the radius is 6 inches and the height is 9 inches.
Substitute the values and solve the equation, like so:
[tex]A=2\pi (6)(9)+2\pi (6)^2=\\A=2\pi (54) +2\pi(36)=\\A=108\pi +72\pi =\\A=180\pi[/tex]
Thus, in terms of pi, the surface area is equal to [tex]180\pi[/tex].
180 times pi is equal to approximately 565.486677646 inches squared.
Peter needs to borrow $10,000 to repair his roof. He will take out a 317-loan on April 15th at 4% interest from the bank. He will make a payment of $3,500 on October 12th and a payment of $2,500 on January 11th.
a) What is the due date of the loan?
b) Calculate the interest due on October 12th and the balance of the loan after the October 12th payment.
c) Calculate the interest due on January 11th and the balance of the loan after the January 11th pa payment.
d) Calculate the final payment (interest + principal) Peter must pay on the due date.
Please only serious answers
Answers
Answer:
A. February 26th
B. $3,500 - Balance ≈ $6,697.26
C. $2,500 - Balance ≈ $4,263.46
D. $4,284.81
Step-by-step explanation:
a) What is the due date of the loan?
The loan term is given as 317 days, and the loan starts on April 15th. To find the due date, we will add 317 days to April 15th.
April 15th + 317 days = April 15th + (365 days - 48 days) = April 15th + 1 year - 48 days
Subtracting 48 days from April 15th, we get:
Due date = February 26th (of the following year)
b) Calculate the interest due on October 12th and the balance of the loan after the October 12th payment.
First, we need to calculate the number of days between April 15th and October 12th:
April (15 days) + May (31 days) + June (30 days) + July (31 days) + August (31 days) + September (30 days) + October (12 days) = 180 days
Now, we will calculate the interest for 180 days:
Interest = Principal × Interest Rate × (Days Passed / 365)
Interest = $10,000 × 0.04 × (180 / 365)
Interest ≈ $197.26
Peter will make a payment of $3,500 on October 12th. So, we need to find the balance of the loan after this payment:
Balance = Principal + Interest - Payment
Balance = $10,000 + $197.26 - $3,500
Balance ≈ $6,697.26
c) Calculate the interest due on January 11th and the balance of the loan after the January 11th payment.
First, we need to calculate the number of days between October 12th and January 11th:
October (19 days) + November (30 days) + December (31 days) + January (11 days) = 91 days
Now, we will calculate the interest for 91 days:
Interest = Principal × Interest Rate × (Days Passed / 365)
Interest = $6,697.26 × 0.04 × (91 / 365)
Interest ≈ $66.20
Peter will make a payment of $2,500 on January 11th. So, we need to find the balance of the loan after this payment:
Balance = Principal + Interest - Payment
Balance = $6,697.26 + $66.20 - $2,500
Balance ≈ $4,263.46
d) Calculate the final payment (interest + principal) Peter must pay on the due date.
First, we need to calculate the number of days between January 11th and February 26th:
January (20 days) + February (26 days) = 46 days
Now, we will calculate the interest for 46 days:
Interest = Principal × Interest Rate × (Days Passed / 365)
Interest = $4,263.46 × 0.04 × (46 / 365)
Interest ≈ $21.35
Finally, we will calculate the final payment Peter must pay on the due date:
Final payment = Principal + Interest
Final payment = $4,263.46 + $21.35
Final payment ≈ $4,284.81
Determine the type of variable for:The number of counties in California.
Qualitative nominal
Quantitative Continuous
Qualitative ordinal
Quantitative discrete
Determine the type of variable for: The stages of childhood: Infant, Toddler, Preschooler, School age, Preteen, Teen
Qualitative nominal
Quantitative Continuous
Qualitative ordinal
Quantitative discrete
Suppose the average time for a class of 28 students (taken from a campus of 1200 students) to drive to campus was 23 minutes.
Select the choice
In the scenario above, 23 minutes is a parameter/ statistic , because 28 students is a sample/ population.
At a Track field, a coach keeps track of an athletes mile time. The coach reported that the mean mile time of a particular athlete was 7 minutes and the standard deviation of the mile time was 1 minute. Assume that the coach also gave us the information that the distribution of the mile time was bell shaped. Use the empirical rule to find:
What percent of the athlete's mile times are expected to be between 6 minutes and 8 minutes?
What percent of the athlete's mile times are expected to be between 4 minutes and 7 minutes?
What percent of the athlete's mile times are expected to be less than 9 minutes?
Answers
The type of variable for,
a. The number of counties in California: Quantitative discrete.
b. The stages of childhood: Qualitative ordinal.
c. In the scenario above, 23 minutes is a statistic, because 28 students is a sample.
d. Between 6 minutes and 8 minutes: Approximately 68% of the athlete's mile times are expected to be between 6 and 8 minutes, according to the empirical rule.
e. Between 4 minutes and 7 minutes: Approximately 68% of the athlete's mile times are expected to be between 4 and 10 minutes, according to the empirical rule.
f. Less than 9 minutes: Approximately 84% of the athlete's mile times are expected to be less than 9 minutes, according to the empirical rule.
In statistics, variables can be categorized into two types: qualitative and quantitative.
Qualitative variables describe characteristics or qualities that cannot be measured numerically, such as gender or hair color.
Quantitative variables, on the other hand, represent numerical values that can be measured or counted.
There are two types of quantitative variables: continuous and discrete. Continuous variables can take any numerical value within a range, such as age or weight.
Learn more about the type of a variable at
https://brainly.com/question/14501374
#SPJ4
which of the following null hypothesis statistical tests require calculating degrees of freedom? group of answer choices all of the above two-sample t-test chi-squared one-sample t-test
Answers
The two null hypothesis that are correct answer are two-sample t-test and one-sample t-test.
Among the group of answer choices provided, the tests that require calculating degrees of freedom are the two-sample t-test and the one-sample t-test. Both of these tests belong to the t-test family and involve using degrees of freedom to determine the critical t-value.
In summary:
- Null hypothesis: The assumption that there is no significant difference between the sample and population or between two samples.
- T-test: A statistical test used to determine if there is a significant difference between the means of two groups or between a sample and population mean.
- Degrees of freedom: A value used in statistical tests that represents the number of independent values in a data set, which can affect the outcome of the test.
So answer is: two-sample t-test and one-sample t-test.
Learn more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ11
The null hypothesis statistical tests that require calculating degrees of freedom are the two-sample t-test and the one-
sample t-test. The degrees of freedom are necessary to calculate the t-value for these tests. The chi-squared test also
requires degrees of freedom, but it is not a test for a null hypothesis.
The correct answer is: all of the above.
All these tests require calculating degrees of freedom:
1. Two-sample t-test:
Degrees of freedom are calculated using the formula (n1 + n2) - 2, where n1 and n2 are the sample sizes of the two
groups being compared.
2. Chi-squared test:
Degrees of freedom are calculated using the formula (rows - 1) * (columns - 1), where rows and columns represent the
number of categories in the data.
3. One-sample t-test:
Degrees of freedom are calculated using the formula n - 1, where n is the sample size.
The null hypothesis statistical tests that require calculating degrees of freedom are the two-sample t-test and the one-
sample t-test. The degrees of freedom are necessary to calculate the t-value for these tests. The chi-squared test also
requires degrees of freedom, but it is not a test for a null hypothesis.
for such more question on null hypothesis
https://brainly.com/question/4436370
#SPJ11
A sprinkler can water a region with an 8 foot radius. A plant is 4 feet east and 6 feet north of the sprinkler. Is the plant in the sprinkler’s range? Why or why not?
Answers
The plant is not in the sprinkler's range since the distance between the sprinkler and the plant is greater than the radius of the sprinkler's range.
The distance between the sprinkler and the plant can be calculated using the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
In this case, the distance between the sprinkler and the plant is the hypotenuse of a right triangle with legs of length 4 feet and 6 feet:
distance = sqrt(4^2 + 6^2)
distance = sqrt(16 + 36)
distance = sqrt(52)
distance ≈ 7.21 feet
Since the distance between the sprinkler and the plant is greater than the radius of the sprinkler's range (8 feet), the plant is not in the sprinkler's range. Therefore, the plant will not receive water from the sprinkler.
Learn more about Pythagorean theorem here
brainly.com/question/14930619
#SPJ4
g a generic drug is being tested to test its efficacy (effectiveness) at reducing blood pressure in patients with hypertension (a.k.a. high blood pressure). in a randomized, double-blind experiment with 200 patients, 100 are given the name-brand drug (control group) and 100 are given a generic version of the drug (treatment group). in the control group, the average reduction in blood pressure is 15.2 mmhg with a standard deviation of 11.5 mmhg. in the treatment group, there is an average reduction of 14.6 mmhg and a standard deviation of 12.5 mmhg. neither group has any outliers. a researcher claims that this study shows the generic drug is not as effective as the name-brand drug. what would be the reply of a statistician? you have two attempts for this problem so choose wisely. if you do not receive 5 points in the gradebook after submitting this assignment then you have answered incorrectly. make sure to try it again before the deadline.
Answers
A statistician would reply that in order to determine if the generic drug is less effective than the name-brand drug, a hypothesis test needs to be conducted.
The null hypothesis (H0) would be that there is no difference in the average blood pressure reduction between the two drugs, while the alternative hypothesis (H1) would be that the name-brand drug has a higher average reduction in blood pressure than the generic drug.
To test these hypotheses, a t-test would be appropriate since we have two independent samples (control and treatment groups) with known means, standard deviations, and sample sizes. The t-test will provide a p-value, which can be compared to a chosen significance level (e.g., α = 0.05).
If the p-value is less than the significance level, we reject the null hypothesis and conclude that there is a significant difference in the average blood pressure reduction between the two drugs. If the p-value is greater than the significance level, we fail to reject the null hypothesis, meaning we do not have enough evidence to claim that the name-brand drug is more effective than the generic drug.
Learn more about hypothesis:
https://brainly.com/question/10854125
#SPJ11
1. Find the height of the parabolic balloon arch for the prom when the position of the bottom anchors are at x = 3 feet and x = 7 feet.
Answers
The height of the parabolic balloon arch for the prom is 12.25 feet.
Using these assumptions, we can find the equation of the parabola that the arch follows as x = a(y-k)² + h, where (h,k) is the vertex and a is a constant that determines the shape of the parabola. We can find the value of a by using one of the points that the arch passes through, say (3,0):
3 = a(0-k)² + h h = 3 - a(k²)
Similarly, using the other point that the arch passes through, say (7,0):
7 = a(0-k)² + h h = 7 - a(k²)
Equating the expressions for h, we get:
3 - a(k²) = 7 - a(k²) a = -1/4
Substituting this value of a into one of the equations for h, say h = 7 - a(k²), we get:
h = 7 + 1/4(k²)
So the vertex of the parabola is at (h,k) = (7,0), and the equation of the parabola is x = -1/4(y² - 28y + 49).
To find the height of the arch, we need to find the y-coordinate of the vertex, which is k = 0. So the height of the arch is given by the distance between the vertex and the lowest point of the arch, which is the x-intercept of the parabola. To find the x-intercept, we set y = 0 in the equation of the parabola:
x = -1/4(0² - 28(0) + 49)
x = -1/4(49) = -12.25
However, since we are dealing with a physical object, the height cannot be negative. Therefore, we take the absolute value of the x-intercept, which gives us:
| -12.25 | = 12.25 feet
To know more about height here
https://brainly.com/question/10726356
#SPJ4
a kite flying in the air has a 94- string attached to it, and the string is pulled taut. the angle of elevation of the kite is . find the height of the kite. round your answer to the nearest tenth.
Answers
The height of the kite is approximately 68.4 ft.
To solve the problem, we can use trigonometry. We know that the string is the hypotenuse of a right triangle, with the height of the kite as one of the legs. The angle of elevation, which is the angle between the string and the ground, is also given. We can use the tangent function to find the height of the kite:
tan(46°) = height / 94
Solving for height, we get:
height = 94 * tan(46°)
Using a calculator, we get:
height ≈ 68.4 ft
Therefore, the height of the kite is approximately 68.4 ft.
We use the given angle of elevation and the length of the string to set up a right triangle with the height of the kite as one of the legs. Then, we use the tangent function to relate the angle to the height of the kite. Finally, we solve for the height using a calculator and round to the nearest tenth as requested.
Learn more about the height
https://brainly.com/question/28122539
#SPJ4
Complete Question:
A kite flying in the air has a 94-ft string attached to it, and the string is pulled taut. The angle of elevation of the kite is 46 °. Find the height of the kite. Round your answer to the nearest tenth.
12' of framing materical can be used to make a rectangular window with a semicircle top. what are the dimensions for the largest area
Answers
The dimension for the largest area is 181 sq ft.
The rectangle has width. [tex]$w$[/tex] and height [tex]$h$[/tex],and let the radius of the semicircle be [tex]$r$[/tex]. We want to maximize the area [tex]$A$[/tex] of the window, which is given by:
[tex]A= 21 \pi r 2 +wh[/tex]
We also have the constraint that the total length of framing material is 12 feet:
[tex]2r+2w+h=12[/tex]
Solving this equation for [tex]$h$[/tex] we get:
[tex]h=12-2r-2w[/tex]
Substituting this expression for [tex]$h$[/tex] into the equation for [tex]$A$[/tex], we get:
[tex]A= 21 \pi r ^2+w(12-2r-2w)[/tex]
Expanding this expression, we get:
[tex]A= 21\pi r^2 +12w-2rw-2w^2[/tex]
To find the values of [tex]$r$[/tex], [tex]$w$[/tex], and [tex]$h$[/tex] that maximize[tex]$A$[/tex], we take the partial derivatives of [tex]$A$[/tex] with respect to each variable, set them equal to zero, and solve for the variables.
We get:
[tex]\partial r/\partial A=\pi r-2w=0 \Rightarrow r= 2w/\pi[/tex]
[tex]\partial w/\partial A=12-2r-4w=0 \Rightarroww= (6-r)/2= (6-2w/\pi)/2=3- w/\pi[/tex]
Substituting the expression for [tex]$w$[/tex] into the equation for [tex]$r$[/tex], we get:
[tex]r= 2/\pi (3-w/\pi )= 6/\pi - 2/\pi^2w[/tex]
Substituting these expressions for [tex]$r$[/tex] and [tex]$w$[/tex] into the equation for [tex]$h$[/tex], we get:
[tex]h=12-2r-2w=12- (4/\pi)w[/tex]
So the dimensions that maximize the area are:
[tex]w= \pi/2,r= 3\pi /4 ,h= (48-8\pi) / \pi[/tex]
The area of the window is:
[tex]A= (1/2)\pir^2 +wh= (1/2)\pi ( 3\pi/4)^2 + (\pi/2)\cdot (48-8\pi)/\pi = 9\pi/8+24-4\pi\approx 18.1 sq ft[/tex]
For similar questions on dimensions
https://brainly.com/question/28107004
#SPJ11
Therefore, the dimensions of the largest area rectangular window with a semicircle top that can be made with 12' of framing material are approximately 1.55' * 3.38'. The maximum area is: Area = 4.82 square feet.
To find the dimensions for the largest area of a rectangular window with a semicircle top using 12' of framing material, we need to use optimization techniques.
Let's denote the width of the rectangular window as "w" and the height of the rectangular portion as "h". We also know that the semicircle top will have a radius equal to the width of the rectangular portion, so its diameter will be 2w.
The perimeter of the window is given by:
Perimeter = 2w + h +[tex]\pi w[/tex]
Since we have 12' of framing material available, we can write:
2w + h + [tex]\pi w[/tex] = 12
We can rearrange this equation to solve for h:
h = 12 - 2w - [tex]\pi w[/tex]
The area of the window is given by:
Area = w * h + 1/2 * [tex]\pi w^2[/tex]
Substituting the expression for h from the perimeter equation, we get:
Area = w(12 - 2w - [tex]\pi w[/tex]) + 1/2 * [tex]\pi w^2[/tex]
Expanding and simplifying, we get:
Area = 12w - [tex]2\pi w^2[/tex] - [tex]w^2[/tex]
To find the dimensions that maximize the area, we need to take the derivative of the area equation with respect to w and set it equal to zero:
d(Area)/dw = 12 - [tex]4\pi w[/tex] - 2w = 0
Solving for w, we get:
w = 12/(4\pi+2) ≈ 1.55'
Substituting this value back into the perimeter equation, we can find the height:
h = 12 - 2w - \piw ≈ 3.38'
Therefore, the dimensions of the largest area rectangular window with a semicircle top that can be made with 12' of framing material are approximately 1.55' * 3.38'. The maximum area is:
Area ≈ 4.82 square feet.
Learn more about area here:
https://brainly.com/question/29327796
#SPJ11
fractions to decimals
Answers
Answer: 1 is .4
2. is .6
3 is .5
4 is .375
5 is .18
6 is .71
7 is .16
8 is .66 repeating
9 is .91
and 10 is .25
Step-by-step explanation:
to get all these and fractions to decimals in the future just divide the numerator by the denominator in other words the top number by the bottom number
1): 0.4
2): 0.67 or 0.7
3): 0.5
4): 0.37 or 0.4
5): 0.18
6): 0.42 or 0.5
7): 0.17
8): 0.7
9): 0.97 or 1
10): 0.25
15. if the integer n has exactly three positive divisors, including 1 and n, how many positive divisors does n2 have?
Answers
Positive divisors does n2 have are 5.
How to calculate how many positive divisors does n2 have?If an integer n has exactly three positive divisors, including 1 and n, it means that n is a perfect square of a prime number.
The reason for this is that a prime number has only two divisors: 1 and itself. Therefore, if n has exactly three positive divisors, n must be a perfect square of a prime number, since the only divisors of a perfect square are the divisors of its square root, and its square root must be a prime number.
Let's say that n is equal to p², where p is a prime number. The positive divisors of n are 1, p, and n (which is p²).
Now, to find the number of positive divisors of n², we can use the fact that any positive divisor of n² can be expressed in the form [tex]p^k[/tex], where 0 ≤ k ≤ 4 (since n² = p⁴).
Therefore, the positive divisors of n² are:
1, p, p², p³, and p⁴ (which is n²)
So, n² has 5 positive divisors: 1, p, p², p³, and n².
Hence, the answer is 5.
Learn more about positive divisors.
brainly.com/question/30207836
#SPJ11
A rectangular mural measures 890 centimeters by 2891
centimeters. Hailey creates a new mural that is 66 centimeters
longer
Answers
The perimeter of the rectangular mural after increasing the dimensions by Hailey is equal to 7826 centimeters.
Measures of rectangular mural are,
length = 890 centimeters
Width = 2891 centimeters
New mural is 66 centimeters longer.
The new dimensions of the rectangular mural will be,
New length = 890 cm + 66 cm
= 956 cm
New width = 2891 cm + 66 cm
= 2957 cm
The perimeter of the new mural can be calculated by adding up the lengths of all four sides,
Perimeter = 2(length + width)
⇒Perimeter = 2(956 cm + 2957 cm)
⇒Perimeter = 2(3913 cm)
⇒ Perimeter = 7826 cm
Therefore, the perimeter of Hailey's new mural will be 7826 centimeters.
Learn more about perimeter here
brainly.com/question/29334827
#SPJ4
The above question is incomplete , the complete question is:
A rectangular mural measures 890 centimeters by 2891centimeters. Hailey creates a new mural that is 66 centimeters longer. What's is the perimeter of Hailey new mural?
A triangle has two legs measuring 21 cm and 20 cm. Which of the following leg measurement will make a right triangle?
Answers
The leg measurement will make a right triangle is 21 cm.
What is hypotenous?The longest side of a right-angled triangle, i.e. the side opposite the right angle, is called the hypotenuse in geometry.
Pythagorean theorem :
If p be the length of the hypotenuse of a right-angled triangle, q and r be the lengths of the other two sides, then
p² = q² + r²
The lengths of the other two sides of the given right-angled triangle are 20 cm and 21 cm. Put these values in the above theorem to get the desired result.
Now, p² = (20)² + (21)²
= 400 + 441 = 841
i.e. p = √(841) = 29
Therefore the length of the hypotenuse is 29 cm. The right angle traingle is 21 cm.
Learn more about hypotenuse, here:
https://brainly.com/question/28946097
#SPJ1